Quaternion math examples for multiplication |
m →Examples: Added new paragraph after image |
||
| Line 13: | Line 13: | ||
== Examples == | == Examples == | ||
[[File:FloatQ Rotation Example.png|alt=Screenshot of Protoflux]] | [[File:FloatQ Rotation Example.png|alt=Screenshot of Protoflux]] | ||
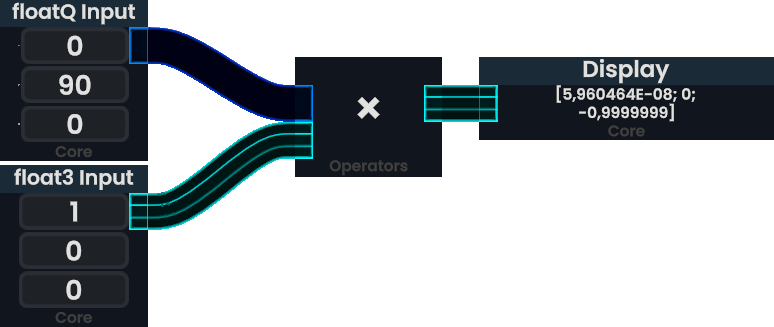
The above [[ProtoFlux|Protoflux]] is rotating a [[Type:Float3|Float3]] vector 90° counter-clockwise around the Y-axis using a FloatQ. This transforms a vector facing towards +X into one towards -Z. Note that the X-component of the output vector is written in [[wikipedia:Scientific_notation|scientific notation]] representing 0.00000005960464. This very small number is the result of precision errors. | The above [[ProtoFlux|Protoflux]] is rotating a [[Type:Float3|Float3]] vector 90° counter-clockwise around the Y-axis using a FloatQ. This transforms a vector facing towards +X into one towards -Z. Note that the X-component of the output vector is written in [[wikipedia:Scientific_notation|scientific notation]] representing 0.00000005960464. This very small number is the result of precision errors. | ||
Revision as of 07:51, 6 February 2024
A FloatQ is a floating point representation of a Quaternion. It is used to represent the rotational component of Slot transforms.
There are four components of a Quaternion:
- x - The first coefficient
- y - The second coefficient
- z - The third coefficient
- w - The fourth coefficient
however, these individual values are not normally used directly.
Quaternion multiplication is not commutative! Multiplying one FloatQ by another will rotate the second FloatQ by the first one, order is important.
Examples
The above Protoflux is rotating a Float3 vector 90° counter-clockwise around the Y-axis using a FloatQ. This transforms a vector facing towards +X into one towards -Z. Note that the X-component of the output vector is written in scientific notation representing 0.00000005960464. This very small number is the result of precision errors.
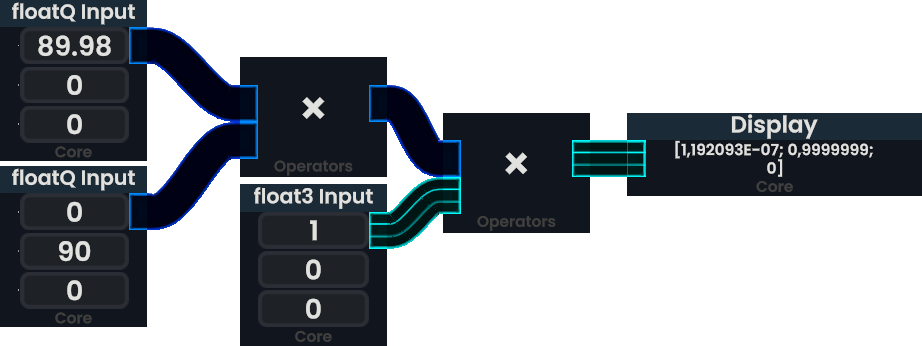
The above Protoflux is first rotating a vector 90° counter-clockwise around the Y-axis and then 90° counter-clockwise around the X-axis. This results in a vector facing towards +Y. The order of the operands is important when rotating a floatQ as it is not commutative. See below for an example.
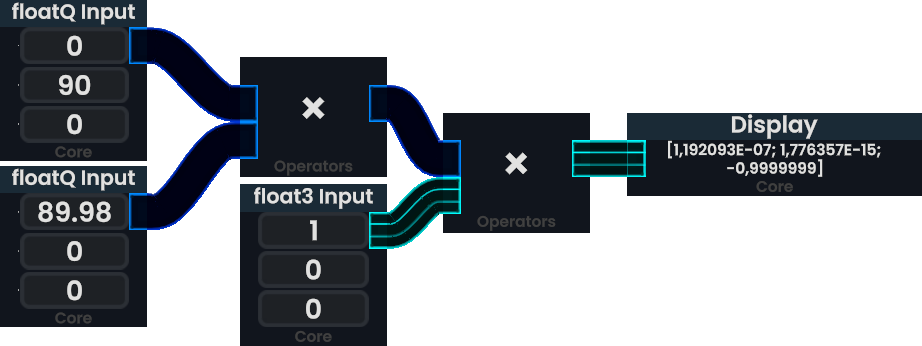
If the operands were swapped, the result would not be different from the first example. To understand this, think of rotating a vector facing towards +X around the X-axis first. The result is the same.== Related types ==