A FloatQ is a floating point representation of a Quaternion, used to represent rotations on things such as Slots.
Overview
The underlying mathematics of a quaternions are complicated and are beyond the scope of this article. That said, Resonite provides plenty of helpers to make working with them more intuitive.
Quaternions are internally made up of four components: X, Y, Z, and W. Since these values are not easy to understand directly, Resonite will usually show quaternions by converting them to and from 3-component Euler angles.
Quaternion multiplication is not commutative! Multiplying one FloatQ by another will rotate the second FloatQ by the first one, order is important.
In ProtoFlux
Rotations With Math
ProtoFlux has specific nodes for working with quaternions, primarily under the Category:ProtoFlux:Math:Rotation category.
Rotations With Matrices
There is a section in ProtoFlux that can let you compose or decompose a rotation using matrices, and that category is Category:ProtoFlux:Operators:Matrix.
Examples
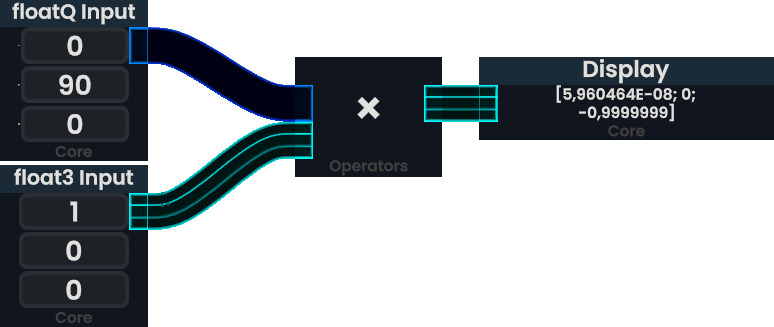
The above Protoflux is rotating a Float3 vector 90° counter-clockwise around the Y-axis using a FloatQ. This transforms a vector facing towards +X into one towards -Z. Note that the X-component of the output vector is written in scientific notation representing 0.00000005960464. This very small number is the result of precision errors.
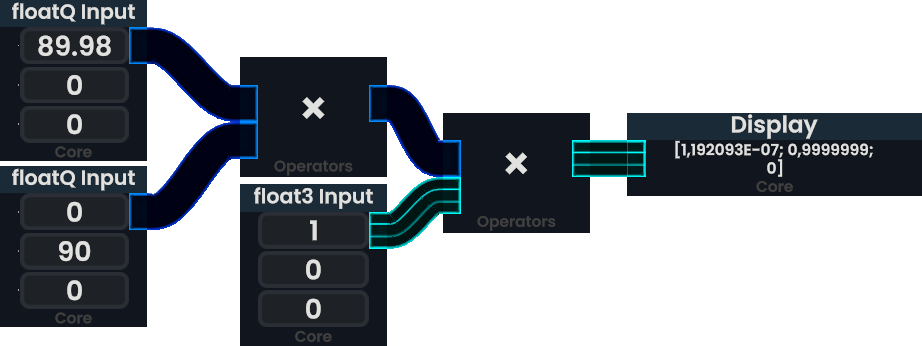
The above Protoflux is first rotating a vector 90° counter-clockwise around the Y-axis and then 90° counter-clockwise around the X-axis. This results in a vector facing towards +Y. The order of the operands is important when rotating a floatQ as it is not commutative. See below for an example.
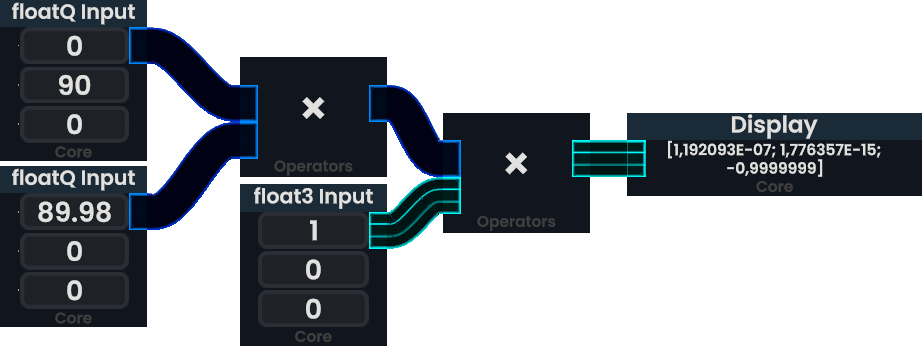
If the operands were swapped, the result would not be different from the first example. To understand this, think of rotating a vector facing towards +X around the X-axis first. The result is the same.
Further Reading
Videos
A video showing how it looks like visually when working with quaternions: